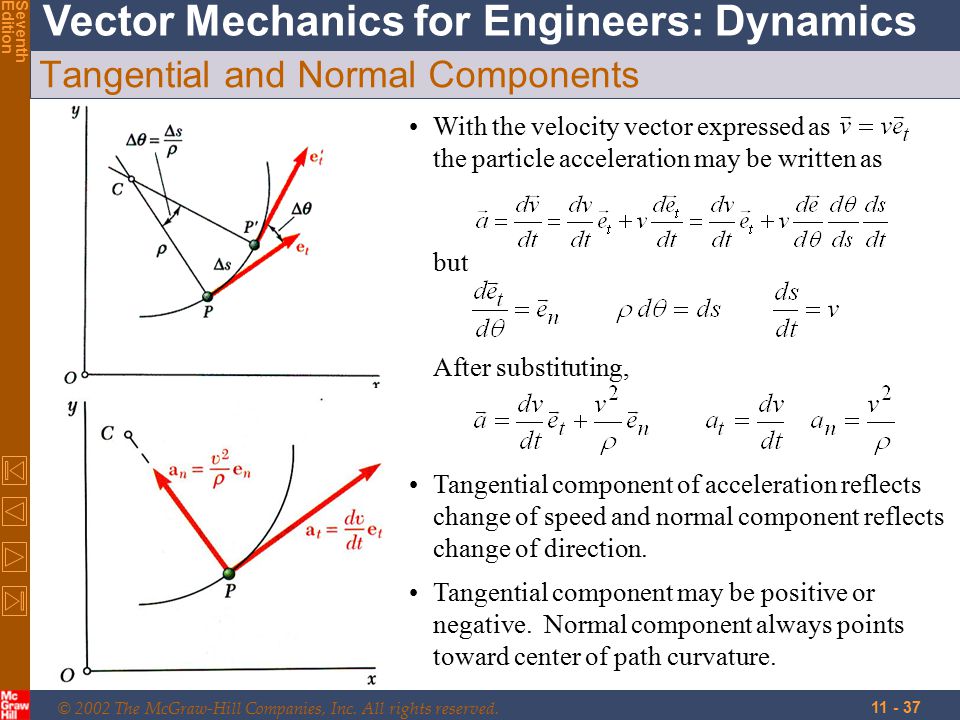
A a t u t a n u n The tangential component is tangent to the curve and in the direction of increasing or decreasing velocity. So there are two components to the acceleration vector.

2 2 0.
Tangential and normal components of acceleration dynamics. Tangential and Normal Components of Acceleration Motion Vectors in the Plane and in Space. Our starting point is using vector-valued functions to represent the position. Components of the Acceleration Vector.
We can combine some of the concepts discussed in. So there are two components to the acceleration vector. A a t u t a n u n The normal or centripetal component is always directed toward the center of curvature of the curve.
A n v2r The tangential component is tangent to the curve and in the direction of increasing or. Since the acceleration is not in general tangent to the path it is useful to express it in terms of components that are normal and tangent to the path. To do so the time derivative of the unit tangent vector et will be found.
Let et t be the unit tangent vector at time t and et t Δt be the unit tangent vector at time t Δt. There are two components to the acceleration vector. A a t u t a n u n The normal or centripetal component is always directed toward the center of curvature of the curve.
A n v2r The tangential component is tangent to the curve and in the direction of increasing or decreasing velocity. A t v or a t. The first type of acceleration is tangential acceleration.
Tangential acceleration only occurs if the tangential velocity is changing in respect to time. To find the tangential acceleration use the equation below. Eq 5 a_tfracv_tdt The second type of acceleration is normal acceleration.
Normal acceleration will always occur when a particle moves through a curved path. Tangential component aT vt d dtrt derivative of speed normal component aN vt2κt quadratic in speed linear in curvature 97. Normal component is always directed toward center of curvature Tangent component is directed toward t or -t direction if speed is increasing or decreasing ME 231.
Dynamics a en et 2 v v. There are two components to the acceleration vector. A a t u t a n u n The tangential component is tangent to the curve and in the direction of increasing or decreasing velocity.
A t v or a t ds v dv The normal or centripetal component is always directed toward the center of curvature of the curve a. The relative normal acceleration component a BA n is 2 r BA and the direction is always from B towards A. A B a A a BA t a BA n The relative tangential acceleration component a BA t is r BA and perpendicular to r BA.
In order to calculate the tangential and the normal acceleration you need to take them as vectors. The angles are theta arctan1612-5313 deg for velocity phi arctan1612-2651 deg for accelaration. Therefore the vectors for acceleration and velocity would be.
And then you can find the component of tangential and normal. As a particle moves around a curved path it can experience a normal and tangential force. First a tangential force is a result of a tangential acceleration which is always perpendicular to radius coming from the axis of rotation.
In order for there to be a tangential force there has to be a change in tangential velocity. In this video our topics -. Tangential and normal components of velocity and acceleration2.
Kinematics and kinetics part 2 link httpsyoutubeZ. A t v d. 2t 2dt 0.
4t ms 2 At t 3s. A t 0. A n v 2 r 0.
2t 2 2 r ms 2 At t 3s. A n 0. 23 2 2 50 0.
0648 ms 2 The magnitude of the acceleration is a a t 2 a n 2 0. 2 2 0. We will study the dynamics of particle motion and bodies in rigid planar 2D motion.
This will consist of both the kinematics and kinetics of motion. Kinematics deals with the geometrical aspects of motion describing position velocity and acceleration all as a function of time. Kinetics is the study of forces acting on these bodies and how it affects their motion.
Example Particle Kinetics with normal and tangential coordinates part 12 - Engineering Dynamics - YouTube. If playback doesnt. Its total acceleration consists of both absolute acceleration and relative acceleration components The relative tangential acceleration component aBAt is a rBA and perpendicular to r_BA.
The relative tangential acceleration component a BA t is r BA and perpendicular to r BA. The relative normal acceleration component a BA n is 2r BA and the direction is. There are two components to the acceleration vector.
A at ut an un The normal or centripetal component is always directed toward the center of curvature of the curve. An v2ρ The tangential component is tangent to the curve and in the direction of increasing or decreasing velocity.