Integral of pi 2

θ d r 12 r 3. π d x π x C.

Once you integrate over r you will get an expression in terms of cos.

Integral of pi 2. Integral 0 to pi2 of xcotx. If playback doesnt begin shortly try restarting your device. The integral of π is no different than the integral of 2.

It is just a constant nothing special. It is just a constant nothing special. π d x π x C.

Neater Shorter Typed Up 2021 Version Here. Httpsyoutube_Ni63fROaQc Get the whole image below. It consists of more than 17000 lines of code.

When the integrand matches a known form it applies fixed rules to solve the integral e. Partial fraction decomposition for rational functions trigonometric substitution for integrands involving the square roots of a quadratic polynomial or integration by parts for products of certain functions. Otherwise it tries different substitutions and transformations until either the integral.

This means π 0 sinxdx cosπcos0 2 0 π sin. X d x c o s π c o s 0 2. Sometimes an approximation to a definite integral is desired.

A common way to do so is to place thin rectangles under the curve and add the signed areas together. Substitute the lower limit in for x x in u 2 x u 2 x. U lower 2 0 u lower 2 0.

Multiply 2 2 by 0 0. U lower 0 u lower 0. Substitute the upper limit in for x x in u 2 x u 2 x.

U upper 2 π 2 u upper 2 π 2. Cancel the common factor of 2 2. Tap for more steps.

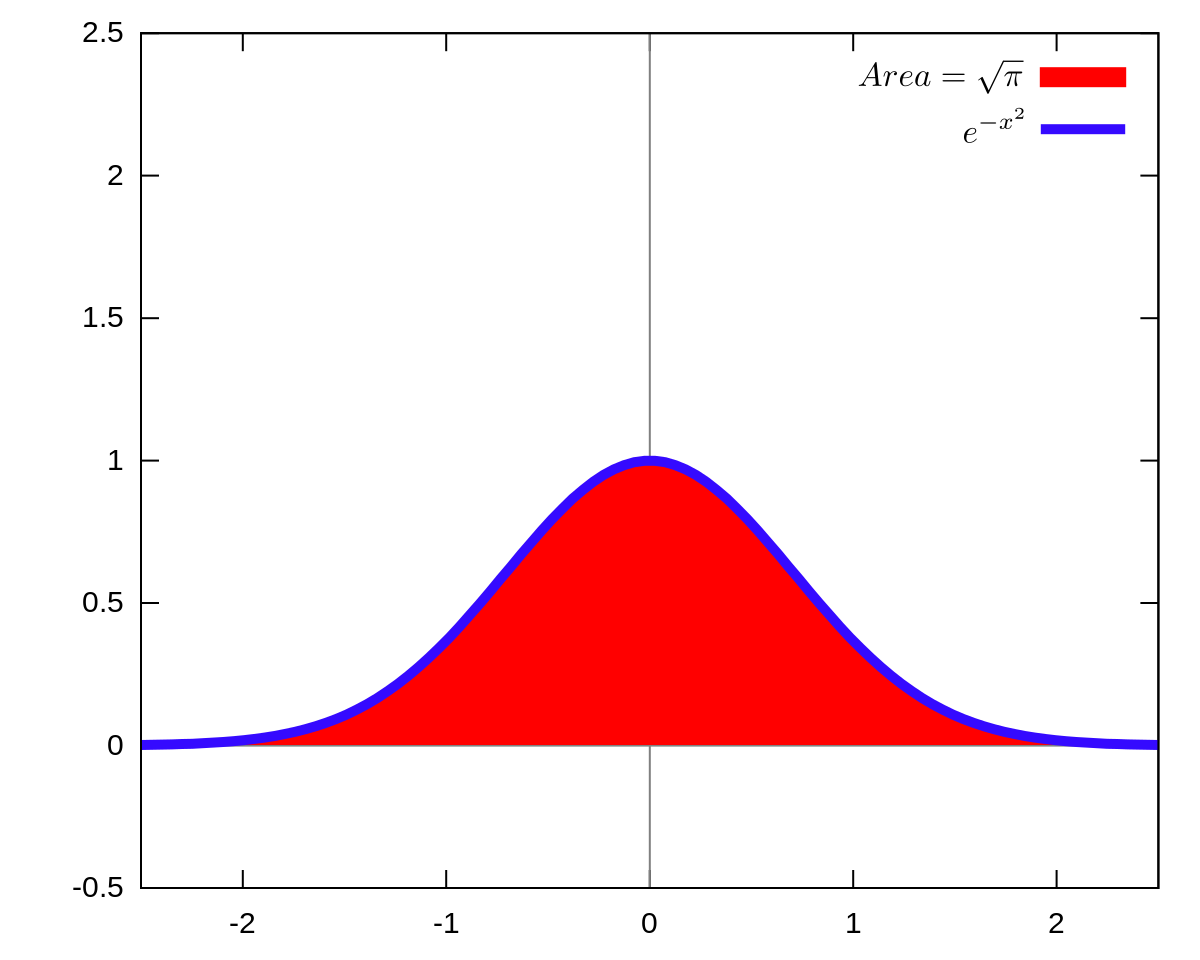
Cancel the common factor. The Gaussian integral also known as the EulerPoisson integral is the integral of the Gaussian function f e x 2 displaystyle fe-x2 over the entire real line. Named after the German mathematician Carl Friedrich Gauss the integral is e x 2 d x π.

Displaystyle int _-infty infty e-x2dxsqrt pi Abraham de Moivre originally discovered this type of integral in 1733 while Gauss published the precise integral. Related Symbolab blog posts. High School Math Solutions Polynomial Long Division Calculator.

Polynomial long division is very similar to numerical long division. In mathematics the definite integral a b f x d x displaystyle int _abfxdx is the area of the region in the xy-plane bounded by the graph of f the x-axis and the lines x a and x b such that area above the x-axis adds to the total and that below the x-axis subtracts from the total. The fundamental theorem of calculus establishes the relationship between indefinite and definite integrals and introduces a technique for evaluating definite integrals.

If A is not an integral multiple of π2 prove that i tanA cotA 2cosec2A ii cot A tan A 2cot2A Prev Question Next Question 0 votes. Asked Nov 18 2019 in Mathematics by SumanMandal 545k points If A is not an integral multiple of π2 prove that i tan A cot A 2 cosec 2A ii cot A tan A 2 cot 2A. Share It On Facebook Twitter Email.

The integrand is even so I would integrate θ from 0 to π 2. This way everything under the square root is a positive quantity so the integral becomes. 2 0 π 2 sin.

θ d θ 0 cos. θ d r 12 r 3. Once you integrate over r you will get an expression in terms of cos.

The the area integral is a double integral over r and the azimuthal angle. The volume integral is over r the azimuthal angle and the polar angle. Youre missing some parts of the big picture about spherical coordinates.

You kind of skipped the intergrating over the azimuthal angle part by including 2 π straight into your integrand. Integral of sin2xcos2x Double angle identity power reduction httpsyoutube6XmbiKGCK14integral of cos2x httpsyoutubeKq8hU80xDPM integral. Stands for the greatest integer function.

Differentiate and equate coefficients. Ye-2xAcos3xBsin3x y-2e-2xAcos3xBsin3xe-2x-3Asin3x3Bcos3xe-2x-2A3Bcos3xe-2x-3A-2Bsin3xe-2xsin3x -2A3B0 -3A-2B1 The solution of the linear equations is Afrac-313 and Bfrac-213 if I did all that arithmetic right which is not very likely so your antiderivative is yxfrac113e-2x-3cos3x-2sin3x and the value of your definite integral. Please subscribe to this channel if you want to get an update when I upload a new video.

Integral of cos xsin7 x - Integral example. Integral of x x212 - Integral example. The answer is e π w 2 but I dont know how do we get it.

E π x 2 cos. 2 π x w d x w R. I encountered this integral when trying to show the Fourier transform of a Gaussian is still a Gaussian.

More specifically e π x 2 e 2 π i x w d x e π x 2 cos. Int sin22pixdx x2 - 18pisin4pix C Use the trigonometric identity. Sin2theta 1-cos2theta2 We have.

Int sin22pixdx int 1-cos4pix2dx using linearity. Int sin22pixdx 12 int dx -12 int cos4pixdx x2 - 18pi int cos4pixd4pix x2 - 18pisin4pix C.