Determine the kernel and range

A Find the kernel and range of the coefficient matrix for the system x -3y 2z a 2x -6y 2w b z -3 w c. 440 443 Let L.

V W is the set of vectors the linear transformation maps to.

Determine the kernel and range. The kernel of a linear transformation L is the set of all vectors v such that Lv 0. Let L be the linear transformation from M 2x2 to P 1 defined by. Then to find the kernel of L we set a d b ct 0 d -a c -b.

So that the kernel of L is the set of all matrices of the form. A the kernel of L is the subset of V comprised of all vectors whose image is the zero vector. KerL v Lv 0 b the range of L is the subset of W comprised of all images of vectors in V.

RangeL w Lv w DEF p. 440 443 Let L. V W be a linear transformation.

Then a L is one-to-one if v1 v2 Lv1Lv2 b L is onto W if range L W. It tells us that the kernel of the transformation T is going to be equal to the span of tea times t minus one the single vector. And this is because the span of this single vector is all in your combinations which would just be constant multiples.

Finally the range of the transformation T is easier to look at notice that we set for T A. KERNEL and RANGE of a LINEAR TRANSFORMATION - LINEAR ALGEBRA - YouTube. T and rng T where T is the linear transformation given by.

R 3 R 3. A 1 1 3 5 6 4 7 4 2. The kernel can be found in a 2 2 matrix as follows.

L a b c d a d b c t. Then to find the kernel of L we set. The Kernel of denoted is the set of all points for which that is.

We will now prove some results regarding the rangekernel of linear operators. Let and be linear spaces and let be a. Determine the kernel and range of each of the following linear operators on mathbbR3.

Beginarrayltext a Lmathbfxleftx_3 x_2 x_. Kernel Rank Range We now study linear transformations in more detail. First we establish some important vocabulary.

The range of a linear transformation f. V W is the set of vectors the linear transformation maps to. This set is also often called the image of f.

Its kernel and range and give the dimension of each. If Tax2bxc ax2bcxabc 0 then clearly a 0 and c b. Thus the kernel of T is the set of all polynomials of the form bxb bx1.

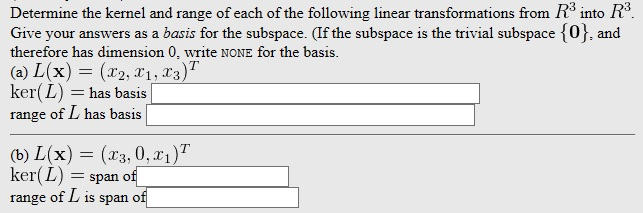
This set has dimension one x1 is a basis. The range of T is all polynomials of the form ax2bcxabc. Determine the kernel and range of each of the following linear transformations from R3 into R3.

Give your answers as a basis for the subspace. If the subspace is the trivial subspace 0 and therefore has dimension 0. Write NONE for the basis.

L x x2x1x3T ker L has basis range of L has basis L x x30x1T ker L span of range. A Find the kernel and range of the coefficient matrix for the system x -3y 2z a 2x -6y 2w b z -3 w c. B Write down compatibility conditions on a b c for a solution to.

View Answer Find bases for the kernel and range of the linear transformations T in the indicated exercises. Here we focus on finding the kernel range rank and nullity of a linear transformation. Using these we will be able to determine if a mapping is one-to-one onto both or none.

A mapping from mathbbR3 to mathbbR3. Find bases for the kernel and range for the linear transformation TR3 to R2 defined by Tx1 x2 x3 x1x2 -2x1x2-x3. To determine whether it is.

By finding relations amongst the elements of LS Lv1 Lvn we can discard vectors until a basis is arrived at. The size of this basis is the dimension of the image of L which is known as the rank of L. Kernel and Range The matrix of a linear trans.

Composition of linear trans. Kernel and Range Motivation In the m n linear system Ax 0. We can regard A as transforming elements of Rn as column vectors into elements of Rm via the rule Tx Ax.

Then solving the system amounts to nding all of the vectors x 2Rn such that Tx 0. The nullity is 1 and a basis for the kernel is the single constant polynomial 1. Since the nullity has dimension 1 and P3 has dimension 4 the range must have dimension 4- 1 3.

Again writing p x a b x c x 2 d x 3 we have as before T p 9 d x 3 6 c x 2 3 d 2 b x 2 c. Solution for Determine the kernel and range for the following transformations. R3 R2 where Tx x1 x2 2x3T.

R2 R2 where Tx. Range and kernel Let VW be vector spaces and L. V W be a linear mapping.

The range or image of L is the set of all vectors w W such that w Lv for some v V. The range of L is denoted LV. The kernel of L denoted kerL is the set of all vectors v V such that Lv 0.

Theorem i The range of L is a subspace of W. The kernel is the same thing in the example youve given ie. So the intersection of the kernel and the range is the kernel itself or equivalently the range itself ie.

Span11 T so in this case clearly the intersection is not 0.